VEKTOR

Umumnya vektor dituliskan sebagai  atau R yang lalu dibaca sebagai vektor R.
Misalkan  dinyatakan dalam koordinat (X₁,Y₁) dapat dituliskan sebagai R = X₁  + Y₁ 
yang mana sumbu-X atau koordinat X dinyatakan dengan vektor satuan  dan sumbu-Y dinyatakan dengan vektor satuan 

Misalkan koordinat R berada pada (3,4) maka cara penulisan vektor menjadi  = 3  + 4 

Menghitung panjang vektor atau ditulis  = 
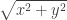
Isikan simbol X dan Y dengan angka.

Misal : Hitunglah panjang vektor dari  = 3  + 4 
Maka cara menyelesaikannya  =  = 5 satuan

Bagaimana jika koordinat R mengandung tiga sumbu ?

Penulisan koordinat R adalah (X, Y, Z)yang dalam vektor dituliskan menjadi  = X  + Y  +Z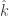 

Untuk menghitung panjang vektor menjadi  = 

Coba lakukan perhitungan dengan 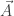 =  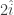+  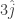+  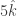terhadap  =   –   +  

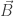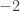
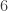
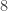
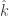
Lakukan :

(a)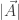 
(b) 
(c)  + 
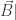
(d)  – 
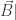
(e)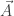  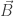  {perkalian titik}
(f)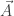  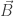  {perkalian silang}

Perkalian Vektor Secara Silang :

 =  (3  8 – (5)  (-6) +  (5  (-2) – 2  8 ) +  ( 2  (-6) – 3  (-2))
=  (24 + 30) +  (-10 – 16) +  (-12 + 6)
=  (54) +  (-26) +  (-6) atau
= 54  -26  – 6